ALGORITMA DAN PEMOGRAMAN KELAS 8
Algoritma dan Pemrograman
Pengertian Algoritma: Algoritma adalah langkah-langkah
atau urutan instruksi yang jelas dan terstruktur untuk menyelesaikan suatu
masalah atau mencapai tujuan tertentu. Algoritma dapat diterapkan dalam
berbagai bidang, tidak hanya dalam pemrograman komputer, tetapi juga dalam kehidupan
sehari-hari.
Contoh Algoritma dalam Kehidupan Sehari-hari: Misalnya,
algoritma untuk membuat teh:
1. Ambil cangkir dan teh
celup.
2. Rebus air.
3. Masukkan teh celup ke
dalam cangkir.
4. Tuang air panas ke
dalam cangkir.
5. Aduk dan biarkan
sebentar.
6. Teh siap disajikan.
Jenis-jenis Algoritma:
Ø Algoritma Linear:
o Algoritma linear
adalah algoritma yang langkah-langkahnya dilakukan secara berurutan dari awal
hingga akhir.
o Contoh: Algoritma untuk
mencuci tangan.
Ø Algoritma Percabangan
(Branching):
o Algoritma percabangan
digunakan ketika ada pilihan atau kondisi tertentu yang mempengaruhi jalannya
proses.
o Biasanya menggunakan
perintah seperti IF (Jika) untuk memeriksa suatu kondisi.
o Contoh: Algoritma untuk
menentukan apakah seseorang lulus ujian berdasarkan nilai.
Ø Algoritma Perulangan
(Looping):
o Algoritma perulangan
digunakan ketika suatu proses atau langkah diulang beberapa kali.
o Biasanya menggunakan
perintah FOR, WHILE, atau DO-WHILE.
o Contoh: Algoritma untuk
menghitung jumlah angka dari 1 sampai 10.
Pemrograman:
Pengertian Pemrograman: Pemrograman adalah proses membuat
instruksi untuk komputer agar bisa menjalankan tugas tertentu.
Instruksi-instruksi ini ditulis dalam bahasa pemrograman yang dapat dipahami
oleh komputer.
Bahasa Pemrograman: Bahasa pemrograman adalah bahasa yang
digunakan untuk menulis algoritma dalam bentuk yang dapat dipahami oleh
komputer. Beberapa bahasa pemrograman yang umum digunakan antara lain:
- Python: Bahasa pemrograman
yang sederhana dan mudah dipahami.
- JavaScript: Banyak digunakan untuk
pengembangan aplikasi web.
- C++: Banyak digunakan untuk
pengembangan perangkat lunak dan aplikasi yang membutuhkan kecepatan
tinggi.
- Scratch: Bahasa pemrograman
visual yang cocok untuk pemula.
Struktur Dasar Pemrograman:
Ø Variabel:
o Variabel digunakan
untuk menyimpan data dalam memori komputer. Setiap variabel memiliki nama dan
tipe data.
o Contoh Variabel:
§ x = 5 (Variabel x menyimpan nilai 5)
§ nama = "John" (Variabel nama menyimpan string
"John")
Ø Tipe Data:
o Tipe data menentukan
jenis informasi yang dapat disimpan dalam variabel. Beberapa tipe data yang
sering digunakan adalah:
§ Integer (int): Menyimpan
bilangan bulat (contoh: 5, -3, 100).
§ Float: Menyimpan angka
desimal (contoh: 3.14, -0.5).
§ String: Menyimpan teks
atau karakter (contoh: "Hello", "Python").
§ Boolean: Menyimpan nilai
benar (True) atau salah (False).
Ø Operator:
o Operator digunakan
untuk melakukan operasi pada variabel atau nilai.
§ Operator Aritmatika: +, -, *, /, % (contoh: a + b untuk penjumlahan).
§ Operator
Perbandingan: =, >, <, >=, <=, != (contoh: x > y untuk membandingkan apakah x lebih besar dari y).
§ Operator Logika: and, or, not (contoh: x and y untuk memeriksa apakah x dan y
benar).
Contoh Algoritma dan Pemrograman dalam
Python:
Contoh 1: Algoritma Linear - Menjumlahkan Dua Angka
- Algoritma:
1. Masukkan angka
pertama.
2. Masukkan angka kedua.
3. Jumlahkan kedua
angka.
4. Tampilkan hasil
penjumlahan.
- Pemrograman (Python):
python
Copy
# Menjumlahkan dua angka
angka1 = int(input("Masukkan angka
pertama: "))
angka2 = int(input("Masukkan angka
kedua: "))
hasil = angka1 + angka2
print("Hasil penjumlahan:",
hasil)
Contoh 2: Algoritma Percabangan - Menentukan Lulus atau Tidak Lulus
- Algoritma:
1. Masukkan nilai ujian.
2. Jika nilai lebih dari
atau sama dengan 60, maka tampilkan "Lulus".
3. Jika nilai kurang
dari 60, maka tampilkan "Tidak Lulus".
- Pemrograman (Python):
python
Copy
# Menentukan lulus atau tidak
nilai = int(input("Masukkan nilai
ujian: "))
if nilai >= 60:
print("Lulus")
else:
print("Tidak Lulus")
Contoh 3: Algoritma Perulangan - Menghitung Total Angka
- Algoritma:
1. Mulai dari angka 1
hingga 10.
2. Jumlahkan semua
angka.
3. Tampilkan hasil
jumlah.
- Pemrograman (Python):
python
Copy
# Menghitung jumlah angka dari 1 sampai
10
total = 0
for angka in range(1, 11):
total += angka
print("Jumlah total angka dari 1
hingga 10:", total)
Struktur Dasar dalam Pemrograman:
1. Input:
o Digunakan untuk
menerima data dari pengguna.
o Di Python, input
dilakukan dengan fungsi input().
o Contoh: nama = input("Masukkan nama:
")
2. Proses:
o Langkah-langkah yang
dilakukan oleh program untuk memanipulasi data yang dimasukkan.
o Contoh: Menghitung
jumlah atau rata-rata.
3. Output:
o Digunakan untuk
menampilkan hasil kepada pengguna.
o Di Python, output
dilakukan dengan fungsi print().
o Contoh: print("Halo, " + nama)
Kesimpulan:
1. Algoritma adalah
langkah-langkah sistematis untuk memecahkan masalah.
2. Pemrograman adalah proses
mengubah algoritma menjadi kode yang bisa dijalankan oleh komputer.
3. Pemrograman
menggunakan bahasa pemrograman seperti Python untuk membuat
aplikasi atau program yang dapat melakukan tugas tertentu.
4. Algoritma dan
pemrograman sangat penting untuk mengembangkan aplikasi dan menyelesaikan
masalah secara efisien.
KONVERSI BILANGAN BINER, OCTAL, DESIMAL, HEXADESIMAL
- Bilangan biner (Bilangan berbasis dua, bilangannya: 0,1)
- Bilangan octal (Bilangan berbasis delapan bilangannya: 0,1,2,3,4,5,6,7)
- Bilangan desimal (Bilangan berbasis sepuluh, bilangannya: 0,1,2,3,4,5,6,7,8,9)
- Bilangan hexadesimal (Bilangan berbasis enam belas, bilangannya: 0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F)
Untuk pengertian jenis – jenis bilangan bisa dibaca di post saya sebelumnya.
Konversi bilangan adalah proses mengubah bentuk bilangan satu ke bentuk bilangan lain yang memiliki nilai yang sama. Misal: nilai bilangan desimal 12 memiliki nilai yang sama dengan bilangan octal 15; Nilai bilangan biner 10100 memiliki nilai yang sama dengan 24 dalam octal dan seterusnya.
Mari kita mulai:
Konversi bilangan biner, octal atau hexadesimal menjadi bilangan desimal.
Konversi dari bilangan biner, octal atau hexa menjadi bilangan desimal memiliki konsep yang sama.Konsepnya adalah bilangan tersebut dikalikan basis bilangannya yang dipangkatkan 0,1,2 dst dimulai dari kanan. Untuk lebih jelasnya silakan lihat contoh konversi bilangan di bawah ini;
- Konversi bilangan octal ke desimal.
Cara mengkonversi bilangan octal ke desimal adalah dengan mengalikan satu-satu bilangan dengan 8 (basis octal) pangkat 0 atau 1 atau 2 dst dimulai dari bilangan paling kanan. Kemudian hasilnya dijumlahkan. Misal, 137(octal) = (7x80) + (3x81) + (1x82) = 7+24+64 = 95(desimal).
Lihat gambar:
- Konversi bilangan biner ke desimal.
Cara mengkonversi bilangan biner ke desimal adalah dengan mengalikan satu-satu bilangan dengan 2 (basis biner) pangkat 0 atau 1 atau 2 dst dimulai dari bilangan paling kanan. Kemudian hasilnya dijumlahkan. Misal, 11001(biner) = (1x20) + (0x21) + (0x22) + (1x2) + (1x22) = 1+0+0+8+16 = 25(desimal).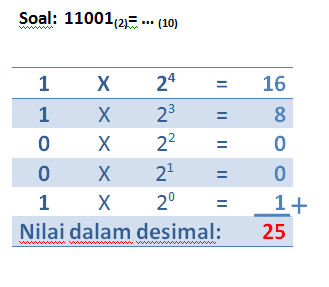
- Konversi bilangan hexadesimal ke desimal.
Cara mengkonversi bilangan biner ke desimal adalah dengan mengalikan satu-satu bilangan dengan 16 (basis hexa) pangkat 0 atau 1 atau 2 dst dimulai dari bilangan paling kanan. Kemudian hasilnya dijumlahkan. Misal, 79AF(hexa) = (Fx20) + (9x21) + (Ax22) = 15+144+2560+28672 = 31391(desimal).
Konversi bilangan desimal menjadi bilangan biner, octal atau hexadesimal.
Konversi dari bilangan desimal menjadi biner, octal atau hexadesimal juga memiliki konse yang sama. Konsepnya bilangan desimal harus dibagi dengan basis bilangan tujuan, hasilnya dibulatkan kebawah dan sisa hasil baginya (remainder) disimpan. Ini dilakukan terus menerus hingga hasil bagi < basis bilangan tujuan. Sisa bagi ini kemudian diurutkan dari yang paling akhir hingga yang paling awal dan inilah yang merupakan hasil konversi bilangan tersebut. Untuk lebih jelasnya lihat pada contoh berikut;
- Konversi bilangan desimal ke biner.
Cara konversi bilangan desimal ke biner adalah dengan membagi bilangan desimal dengan 2 dan menyimpan sisa bagi per seitap pembagian terus hingga hasil baginya < 2. Hasil konversi adalah urutan sisa bagi dari yang paling akhir hingga paling awal. Contoh:125(desimal) = …. (biner)
125/2 = 62 sisa bagi 1
62/2= 31 sisa bagi 0
31/2=15 sisa bagi 1
15/2=7 sisa bagi 1
7/2=3 sisa bagi 1
3/2=1 sisa bagi 1hasil konversi: 1111101
Lihat gambar: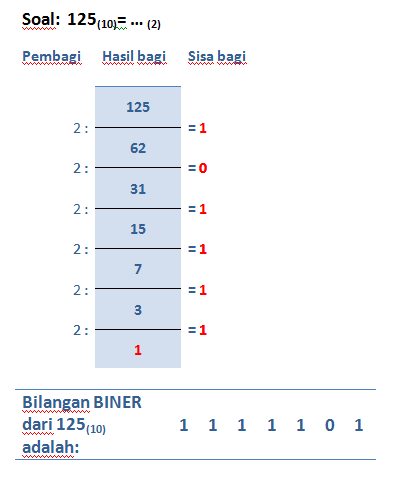
- Konversi bilangan desimal ke octal.
Cara konversi bilangan desimal ke octal adalah dengan membagi bilangan desimal dengan 8 dan menyimpan sisa bagi per seitap pembagian terus hingga hasil baginya < 8. Hasil konversi adalah urutan sisa bagi dari yang paling akhir hingga paling awal. Contoh lihat gambar:
- Konversi bilangan desimal ke hexadesimal.
Cara konversi bilangan desimal ke octal adalah dengan membagi bilangan desimal dengan 16 dan menyimpan sisa bagi per seitap pembagian terus hingga hasil baginya < 16. Hasil konversi adalah urutan sisa bagi dari yang paling akhir hingga paling awal. Apabila sisa bagi diatas 9 maka angkanya diubah, untuk nilai 10 angkanya A, nilai 11 angkanya B, nilai 12 angkanya C, nilai 13 angkanya D, nilai 14 angkanya E, nilai 15 angkanya F. Contoh lihat gambar:
Konversi bilangan octal ke biner dan sebaliknya.
- Konversi bilangan octal ke biner.
Konversi bilangan octal ke biner caranya dengan memecah bilangan octal tersebut persatuan bilangan kemudian masing-masing diubah kebentuk biner tiga angka. Maksudnya misalkan kita mengkonversi nilai 2 binernya bukan 10 melainkan 010. Setelah itu hasil seluruhnya diurutkan kembali. Contoh:
- Konversi bilangan biner ke octal.
Konversi bilangan biner ke octal sebaliknya yakni dengan mengelompokkan angka biner menjadi tiga-tiga dimulai dari sebelah kanan kemudian masing-masing kelompok dikonversikan kedalam angka desimal dan hasilnya diurutkan. Contoh lihat gambar:
Konversi bilangan hexadesimal ke biner dan sebaliknya.
- Konversi bilangan hexadesimal ke biner.
Sama dengan cara konversi bilanga octal ke biner, bedanya kalau bilangan octal binernya harus 3 buah, bilangan desimal binernya 4 buah. Misal kita konversi 2 hexa menjadi biner hasilnya bukan 10 melainkan 0010. Contoh lihat gambar:
- Konversi bilangan biner ke hexadesimal.
Teknik yang sama pada konversi biner ke octal. Hanya saja pengelompokan binernya bukan tiga-tiga sebagaimana pada bilangan octal melainkan harus empat-empat. Contoh lihat gambar:
Konversi bilangan hexadesimal ke octal dan sebaliknya
- Konversi bilangan octal ke hexadesimal.
Teknik mengonversi bilangan octal ke hexa desimal adalah dengan mengubah bilangan octal menjadi biner kemudian mengubah binernya menjadi hexa. Ringkasnya octal->biner->hexa lihat contoh,
- Konversi bilangan hexadesimal ke octal.Begitu juga dengan konversi hexa desimal ke octal yakni dengan mengubah bilangan hexa ke biner kemudian diubah menjadi bilangan octal. Ringkasnya hexa->biner->octal. Lihat contoh;














